Sports Betting: Learning From the Original Prediction Markets

Dec 26, 2022

Introduction

I’ve been interested in prediction markets for a while, and have a lot of questions about how they work that I think could be answered through some pretty simple data analysis. Unfortunately, there aren’t a lot of publicly available datasets for sites like PredictIt, Manifold Markets, etc. I previously did a project where I collected data from these sites myself and analyzed accuracy for the 2022 midterms, but this approach has some limitations – the data collection is very tedious and can only be done in the present, and would have to be done for several years to see if a trend repeats itself.

Something that occurred to me, though, is that maybe some of my questions could be answered by looking at data from sports betting markets. They’re basically the original prediction markets – based on the same fundamental principles as political prediction markets, except they’ve been around much longer, are less controversial, more legal, and have tons of publicly available data.

In this post, I’ll try to answer a question about prediction market efficiency by comparing data from sports betting markets to forecasts made by Nate Silver (of the famous forecasting site FiveThirtyEight).

Are Prediction Markets Efficient?

When I say “efficient” here, I’m not using it as a synonym for “good,” “fair,” or some other value judgment. I’m using the word in the sense of the Efficient Market Hypothesis (EMH). According to the EMH, when financial assets are traded under the right conditions (enough traders, low barriers to entry, etc), their prices will reflect all available information about the underlying financial value of the assets.

The idea is that if there was some piece of information that wasn’t already reflected in the asset price, there would be a financial incentive for anyone who knows this information to make the appropriate trades based on it, thus pricing in the information.

There’s a famous but inaccurate economics joke about the EMH, which has since been corrected by an extremely unfunny but more accurate version of the joke - reading these might be helpful in understanding the concept.

How do we know if a market is efficient? Well, we can never really be sure. But there are ways to spot if a market is inefficient. For example, a corollary of the EMH is that it should be impossible for an expert’s predictions to consistently outperform the market in the long run (other than due to luck), because if this were happening, then there would be an incentive for people to start trading based on this expert’s predictions, thus pricing in the information and eliminating the market inefficiency. So if we see an expert making predictions that consistently outperform the market again and again, that probably means the market is inefficient – unless we’re making a probabilistic fallacy that causes us to interpret luck as impressive skill in hindsight.

So, are prediction markets efficient? Scott Alexander addressed this in his recent Prediction Market FAQ – and he says yes, at least when the market is operating under the right conditions. The problem, according to Scott, is that a lot of the prediction markets are not operating under these ideal conditions. For example, it’s somewhat well known that PredictIt tends to have a slight conservative bias and consistently underprices the Democrats’ chances of winning. Scott mentions that he typically makes a couple hundred bucks per election cycle by betting counter to this inefficiency (and not to brag, but so do I actually).

Also, I recently did an analysis of forecast accuracy for the 2022 midterm elections, and found that Nate Silver outperformed PredictIt overall. This is not a solid confirmation of the market inefficiency, since it was only based on one year, but it’s a piece of evidence that supports what Scott and many others have anecdotally observed.

But according to Scott, this inefficiency only exists because PredictIt has a $850 cap on how much you can bet – if it weren’t for this cap, someone would take advantage of knowing about this inefficiency to make a much larger bet, enough to price in the information.

I find this to be a convincing theoretical argument, but it would be nice to have some data to test it. This is where the sports betting data comes in.

Results

In addition to election forecasts, FiveThirtyEight (Nate Silver’s site) also makes forecasts about sports games. One great thing about FiveThirtyEight is that they make all of their forecast data available online, for anyone to analyze, so I was able to get ahold of their predictions for the 2016-2020 MLB, NFL, and NBA seasons. These datasets included forecast probabilities for every game in each season – forecasts for several thousand games total.

I was able to get ahold of some sports betting odds datasets for the 2016-2020 MLB, NFL, and NBA seasons from Sportsbook Reviews Online, which has an impressive archive of data for a variety of sports. Again, I’m looking at the odds for each game in each season.

[QUICK METHODOLOGY NOTE – in sports betting, the odds are purposely set up in a way that the raw implied probabilities sum to greater than 1 (usually like 1.02 or so) [credit to u/wstewartXYZ on reddit for correcting me on this], so that the bookies are guaranteed to make money regardless of the outcome. I decided to correct this for my analysis, and normalize the implied probabilities so that they sum to 1. I think this makes sense in terms of comparing prediction accuracy, but if anyone has a good counter-argument for why I should not do this, please let me know and I’ll consider it.

(By the way, do you guys know what I mean when I’m talking about odds and their implied probabilities in this context? Right now I haven’t written a methods section for this post, but if people are confused about this let me know and I’ll write up a methods section explaining it.)]

[ANOTHER METHODOLOGY NOTE – when I did my previous analysis of the midterm forecasts, I made sure to collect the data from all sites at the same time (give or take 15 minutes or so), in order to have a solid apples-to-apples comparison between sites. Unfortunately with this analysis of sports betting and forecasts, I don’t know the exact time that these odds and forecasts were recorded, so there is some possibility of bias in timing. With that being said, I think the results are informative even when we factor this consideration in.]

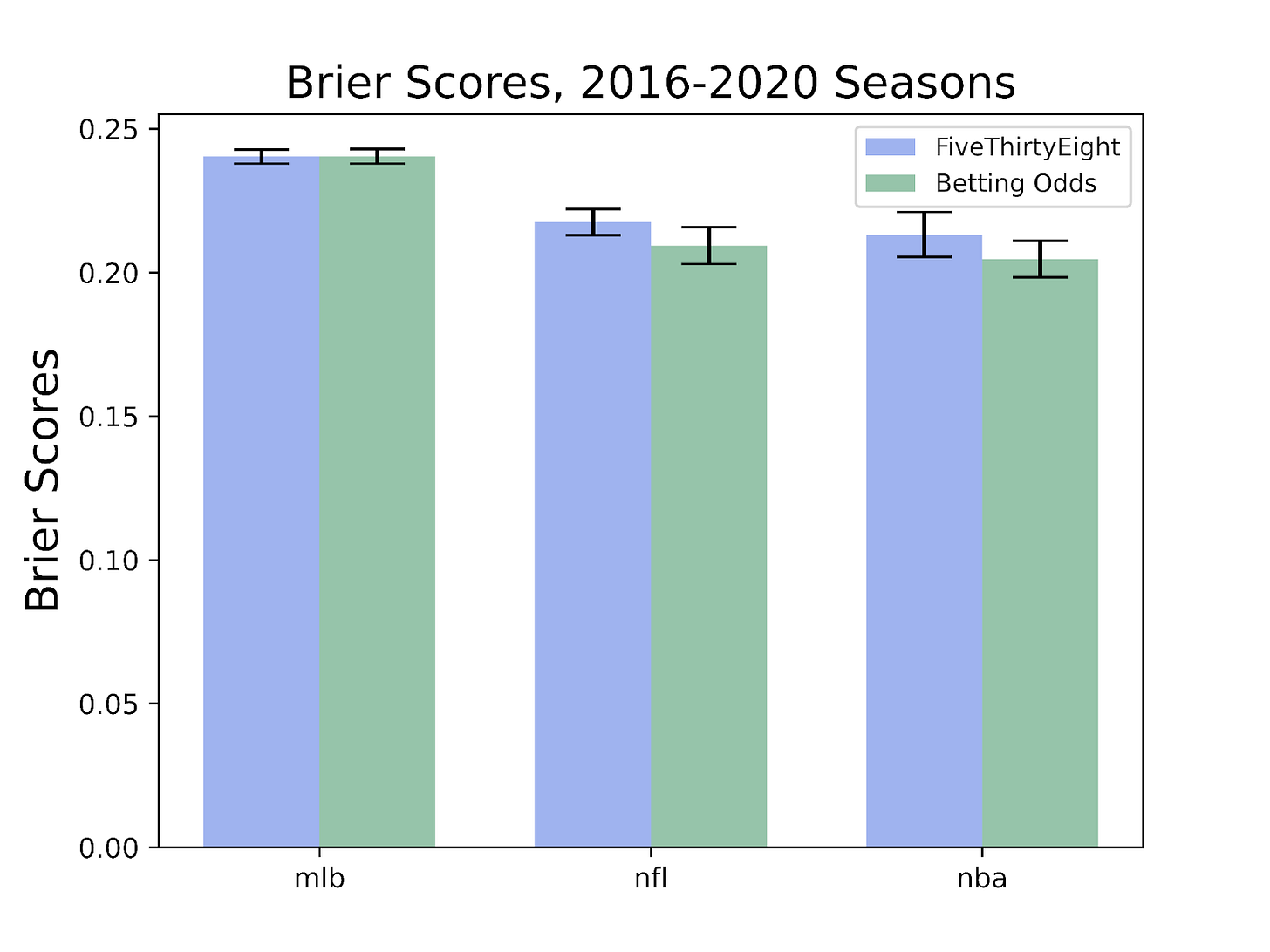
Anyway, here are the results comparing FiveThirtyEight to the betting market data, for the 2016-2020 seasons of the MLB (baseball), NFL (football), and NBA (basketball). Please note that Brier scores are a measure of error, so lower scores are better here.

As you can see, Nate Silver does nearly as well as the betting markets, but is not able to consistently outperform them in a way that would suggest a market inefficiency.

Here are the results in a bar graph, with error bars showing one standard deviation:

Do you guys remember that lesson from 7th-grade science class about how we never actually “accept” a hypothesis, but rather we “fail to reject” it? I think that kind of language is appropriate here. Based on this analysis, we can’t accept that sports betting markets are efficient, but so far we have failed to reject this hypothesis. Or to put it in Bayesian terms, these results warrant some update in favor of the efficient market hypothesis being true for sports betting markets.

Reasons Why This Might Not Extrapolate to Political Prediction Markets

Even though the whole point of this post is to attempt to learn about prediction markets by studying sports betting, I think it’s important to be cautious here. It’s appropriate to update our beliefs in the direction of thinking prediction markets are efficient in general (when operating under the right conditions, like no bet size limits), but this is far from being a rock-solid confirmation.

For one thing, it’s possible that a prediction market could be biased because of a selection effect related to the type of people who trade in the market (this could be true even in the absence of bet size limits and legal barriers to entry) – and it seems like this kind of selection effect could affect political prediction markets like PredictIt more than it affects sports betting.

For example, probably most traders in both sports betting markets and political prediction markets are men. In political prediction markets, this could cause the markets to skew slightly conservative in a consistent way – especially if the prediction markets attract men who are interested in finance and economics. On the other hand, it’s more difficult to see how sports betting markets being primarily made up of men would bias the market in favor of some teams over others.

This is just speculation. Anyway, the point is there could still be some differences between sports betting markets and political prediction markets (other than just betting caps, market size, and legal barriers to entry), that could lead to sports betting markets being efficient in a way that sites like PredictIt aren’t – so we need to be very cautious about extrapolating here.

[SIDE NOTE – one possible bias I can think of for sports betting markets is that teams with larger fanbases may have more people betting on them to win compared to teams with smaller fanbases, biasing the forecast probabilities in favor of the more popular team. For example, when the NY Yankees are playing the Milwaukee Brewers, it could be that the Yankees’ chances of winning are consistently overestimated simply because they have a much larger fanbase and more fans betting on them to win. I’d like to do an analysis to see if this is true, and either write up the results in a report or (if it is true) maybe just keep it to myself and try to make some money lol.]

Another Interesting Result

Unrelated to the efficient markets question, but during this analysis I also noticed that some sports seem to be inherently more predictable than others. Here’s a plot of Brier scores for the betting markets from 2016-2020, with error bars showing one standard deviation. This plot includes the sports I mentioned before, as well as the NHL (hockey) and NCAA football (this is a college football league, in case anyone reading this is unfamiliar).

I think this result is somewhat interesting. Some sports like hockey and baseball are apparently hard to predict, while NCAA football is pretty predictable by comparison.

Conclusion

This analysis has failed to disprove the efficient market hypothesis for sports betting. We need to be very cautious about extrapolating results from sports betting to political prediction markets, but I think it does warrant some update in favor of the EMH being true for prediction markets in general, under the right conditions.

Data and code for this analysis are available on my Github.

I’m probably going to keep writing about forecasting and prediction markets in my free time, so if you’re interested in reading more about this please subscribe (for free)! And if anyone has any specific analyses they’d like to see or questions they’re interested in, please let me know and I’ll work on answering them.

Thanks for reading!

Mike’s Blog

Discussion about this post